二八法则与长尾理论
我不知道上帝抽什么牌子的香烟,但是有一点我敢肯定,那就是他在写 hello world 这个程序的第一个版本时用了不少递归,原因是这样可以节省不少力气。(这个家伙很懒,在写 Women 这个 class 的时候继承了 Man。)
最好的证明就是山河湖泊风花雪月悬崖峭壁中隐藏的那些分形,和现实生活中比比皆是的幂律幂律分布。
关于幂律分布(power-law distribution),生活中有许多有趣的现象,比如我们非常熟悉的长尾理论,80/20 法则和 Zipf 定律。
长尾理论
长尾(The Long Tail)这一概念是由 Wired 杂志主编 Chris Anderson 在 2004 年十月的 The Long Tail 一文中最早提出,用来描述诸如 Amazon 这类网站的商业和经济模式。
市场上流通的图书高达 300 万种,但能够登上新华书店畅销书架上的幸运儿终究是少数,而其他书大多躺在了书店的角落,无人问津。直到 Amazon 的出现,非畅销书作者们才迎来了他们的春天。Amazon 每年在“小众”图书上取得的盈利总和远远超过了那几本畅销书带来的利润。所谓聚沙成塔,就是这个道理。
众所周知,Google 的摇钱树 AdSense 就是通过对数以百万计的中小型网站和个人网站提供广告个性化的广告服务,将这群“乌合之众”汇集在一起,组成了一支规模庞大的正规军,带来了巨大的经济价值。
当互联网进入 2.0 时代以后,所有用到机器学习算法做用户推荐的网站,都可以看成是对长尾理论的很好利用,即寻找长尾端“小众”用户的需求。比如在豆瓣上,你发现一本书有 10 个人“在读”时带来的惊喜远比你发现一本书有 1 万人在看要强烈得多。推荐一部正在热映的电影的意义也远不及推荐一部上世纪 60 年代由莫斯科电影厂出品但是很对你口味的片子。
80/20 法则
80/20 法则又称“二八”定律。是20世纪初意大利统计学家、经济学家 Vilfredo Pareto 提出的,简单来说就是:社会上 80% 的社会财富被 20% 的人所拥有。
在犹太人社区中也流传着类似的说法,叫78∶22 宇宙法则,即世界上许多事物,都是按 78∶22 这样的比率存在的。比如空气中,氮气占 78%,氧气及其他气体占 22%。人体中的水分占 78%,其他为 22%等等。
Bruce Eckel 在 Mythical 5% 这篇文章中指出:5% 的程序员开发效率是其他 95% 程序员的 20 倍。
但也有人说 80/20 法则已经过时了,而另一条新的经验法则正在逐渐成型,那就是如果在互联网上的每 100 人中,只有 1 个人会创造内容,10 个人会参与互动而余下 89 人仅仅是浏览。也就说即使是在 web2.0 时代,舞台上的终究是少数,大多数人都在打酱油。
Zipf
1932 年,哈佛大学的语言学专家 Zipf 在研究英文单词出现的频率时,发现如果把单词出现的频率按由大到小的顺序排列,则每个单词出现的频率与它的名次的幂次存在简单的反比关系。这说明:英语单词中只有少数的词被经常使用,而绝大多数词很少被使用。
事实上 Zipf 定律这在汉语中也成立,对于一个普通人来说认识常用字 2500 字就足以完成写情书、催债信等的艰巨任务了,认识 900 个字也可以看看报纸了。而一篇文章中反复出现次数最多的汉字可能只有 50~100 个,我小时候就是从写这些字开始的。
英国的海岸线有多长
1967年,一篇大标题叫 How Long is the Coast of Britain 的 paper 在 Science 上发表,引起了一阵骚动。作者 Beonit Mandelbrot 是一位美籍法裔的数学家和计算机科学家,当时正在纽约的 IBM 公司的 Watson 研究中心工作。 他给出的答案令人瞠目:无论你做得多么认真细致,你都不可能得到准确答案,因为根本就不会有准确的答案。英国的海岸线长度是不确定的!
原来,海岸线由于海水长年的冲涮和陆地自身的运动,形成了大大小小的海湾和海岬,弯弯曲曲极不规则。
假如你乘一架飞机在 10000m 的高空沿海岸线飞行,同时不断拍摄海岸照片,然后按适当的比例尺计算这些照片显示的海岸总长度,其答案是否精确呢?否!因为,你在高空不可能区别许多的小海湾和小海峡。如果改乘一架小飞机在 500m 高处重复上述的拍摄和测量,你就会看清许多原来没有看到的细部,所测得的结果就会大大增加。
随着测量尺度的不断减小,你观察到的细节足够多,海岸线就会越来越长。最终你所需要做的一件事就是拿着一把无穷小的尺,进行无穷多次的测量。
分形
关于分形,Mandelbrot 曾说过:
无论从美学的观点还是从科学的观点,许多人在第一次见到分形时都有新的感受。
Wikipedia 的定义是:
分形通常被定义为“一个粗糙或零碎的几何形状,可以分成数个部分,且每一部分都(至少近似地)是整体缩小后的形状”,即具有自相似的性质。
由于这种自相似的性质,无论我们在哪个尺度上观察分形,结果都是相同的。
也就是说,无论站在怎样的尺度上观察,分形系统的构造都是相同的,这导致观察者说不出自己究竟在分形的哪个尺度上。而这就是所谓的尺度不变性(scale free)。这恐怕是分形如此迷人的根本原因。
现实世界的很多东西满足分形的这种自相似性,但前提是,在一定的范围以内。比如我们在显微镜观察一片叶子,并且不断提高放大倍数,最后看到的分子,而不再是之前的递归结构。
尺度不变性
通过幂律分布公式同样可以得出尺度不变的结论。
\[f(cx) = a(ck)^k= c^kf(x)\propto f(x)\]当我们把 x 变为原来的 c 倍时,f(cx) 与 f(x)成正比。
假设人类个体财富满足这个式子:财富 = 1000 * (人口) ^ -1,那么它满足幂律分布,也就是所谓的“80/20 法则”:财富达到 1000¥的人仅有 1 个,而有 1000 人只有 1¥。
当我们从人口数量这个角度去观察系统的结构时,会发现:无论站在哪个尺度上,观察到的系统都是相同的。
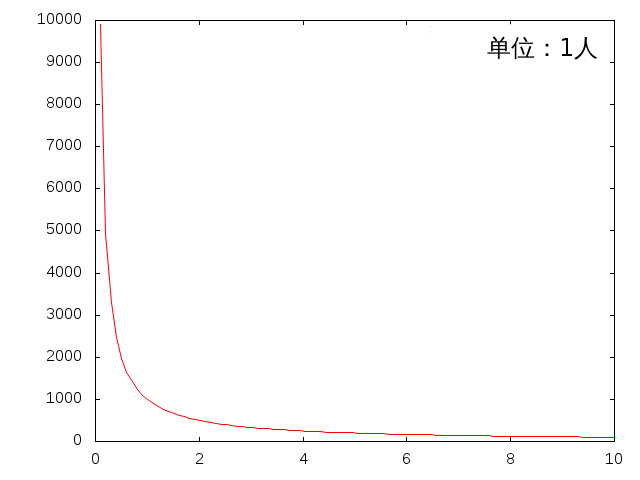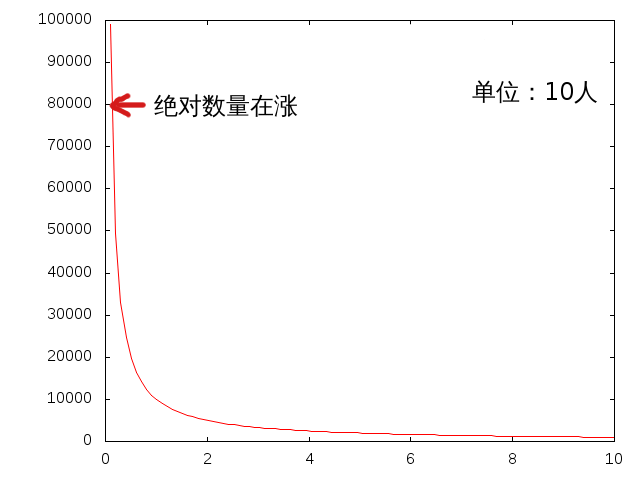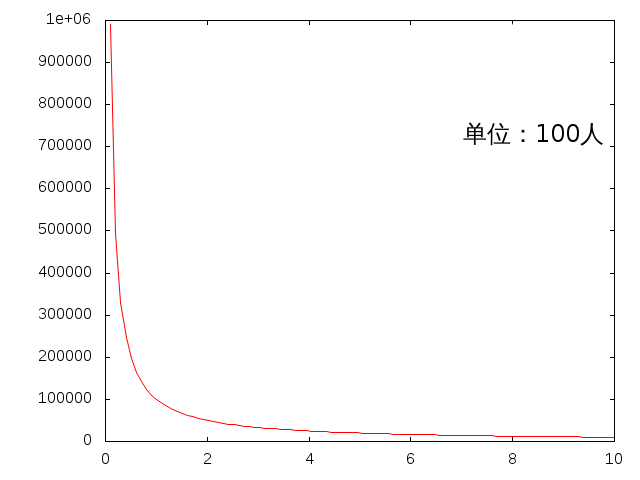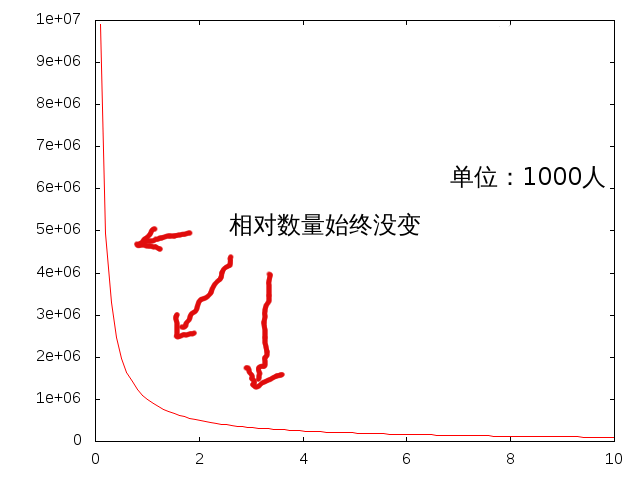
尽管,在不同尺度的人口数量下财富的绝对数量还是发生了明显的变化,但是相对量却没有变。事实上,一旦我们把 CPI、通货膨胀、汇率问题、攀比心理种种因素考虑进去,财富的绝对数量也就失去了意义。
这说明人类财富的分配存在着某种自相似性,以至于当你变换观察的尺度时,整个系统看起来都没有太大的变化。无论你是站在一个人的角度看,还是一户人家,甚至是一个国家,财产都是这么分布的。这些分布是如何产生的?除了递归,我想不到其他解释。
相反,如果人类个体财富与人口之间的关系不满足幂律,而是一个正弦函数(财富数量 = sin (人口数量))的话,情况就截然不同:
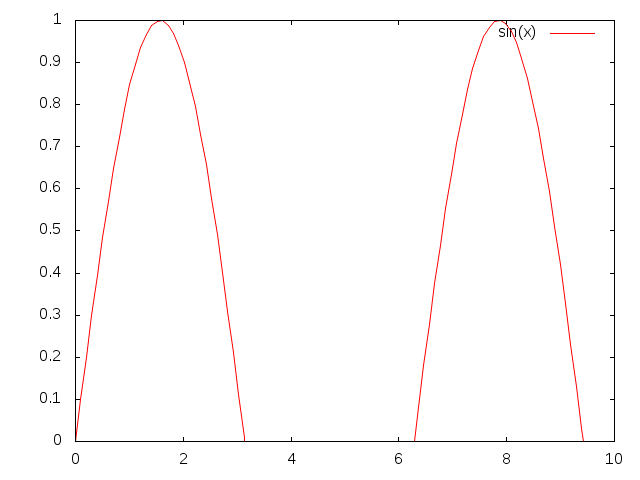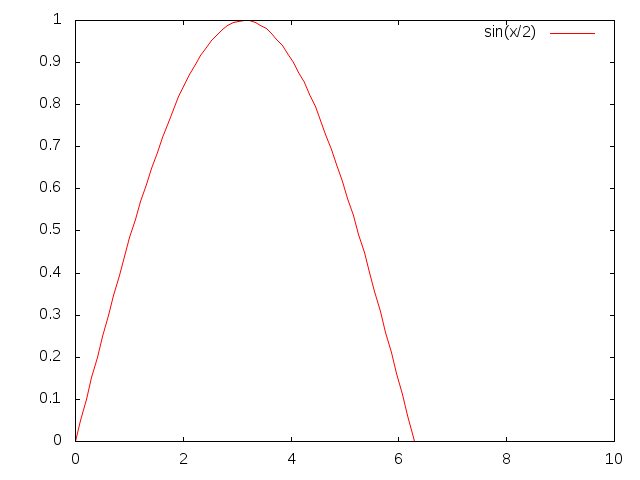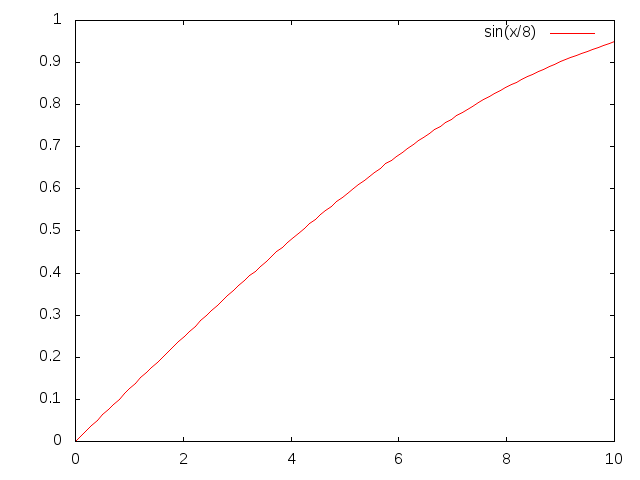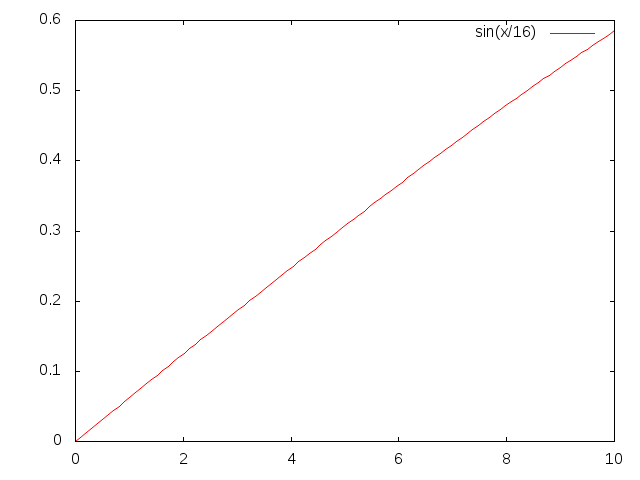
当我们不断改变人口数量的尺度时(每次以之前两倍的比例尺),观察到的系统明显不同。
形而上
纵观整个世界,物质的构成都是分层次的,大到一个星系,小到一个原子核,莫不如是。如果要为每一种物质的生成和运动规律写一段代码,上帝非累死不可,那么最好的办法就是用递归。于是这个世界在不同的层次上存在着不同程度的自相似,比如物体运动的规律在很大的范围内都适用。而在很长一段时期我们人类因为没有望远镜,也没有显微镜,所以一直在以一个很有限的尺度观测周遭的这个宇宙。
Jonathan Swift 在小说 Gulliver’s Travels 中有过这样的描写,当 Gulliver 来到巨人国后,他发现没有一个女人是漂亮的,因为在他小小的眼睛里,女人每一个狰狞的毛孔他都看得清清楚楚。这说明一个女人是否美丽,除了黄金分割,还要把观察者的尺度考虑进去。
递归的深度 n 取决于上帝创世纪之初时使用的那台 Adam-I 的配置,人类花了 10 万年的时间进化到今天的程度,当中走了不少弯路,直到最近100年科技突飞猛进,已经从宏观和微观两个方向探测到了多个 n 的值,从而证明他那台计算机的性能也不过如此。
如果让我猜一猜生命最初那段代码是啥,我觉得很有可能是 Theory_of_Evolution()。大自然界中充斥着适者生存,物竞天择,个体除了面临如何生存的问题,更是肩负着繁衍种群后代的使命。我们每个人都包孕在整个人类的文明之中(不同的上下文,但却是同样的代码片段)。所以不要问我丧钟为谁而鸣,它也为你敲响。